Pricing

When a Harbor market is presented with a bond to buy or sell, it makes use of an on-chain pricing algorithm which generates a quote based on the attributes of the bond, such as the amount of tokens locked up in the bond, the time to maturity, the issuer, and/or other attributes.

Let:

• $P_b(t)$: the buy price of the bond at time $t$
• $P_s(t)$: the sell price at time $t$
• $V$: the face value (redemption value) of the bond at maturity $T$
• $P(t)$: the market price function returned by the pricing algorithm

Then, to guarantee profitability and arbitrage safety, the pricing algorithm should satisfy:

$$P_b(t) < P_s(t) < V \quad \forall t < T$$

Additionally, prices must not decrease over time:

$$\frac{dP(t)}{dt} \geq 0$$

If a bond is purchased but not resold, the maximum profit is realized at redemption:

$$\Pi(t) = V - P_b(t)$$

where $\Pi(t)$ is the profit if the bond is held to maturity.

Consider the following Linear strategy.

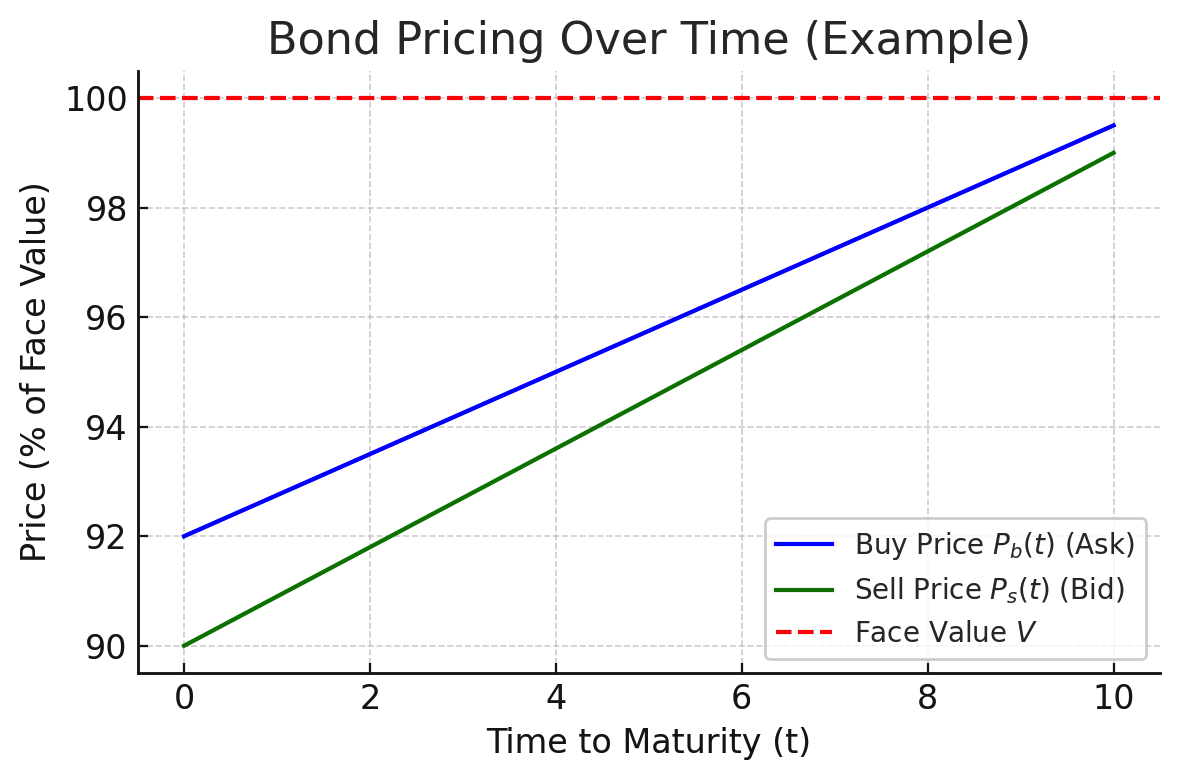
Example Linear pricing strategy demonstrating how bond prices increase linearly from purchase price to face value over time